Euler's Method
The geometric concept of a slope field, from the last section, is closely related to a fundamental numerical method for approximating solutions to an initial value problem for a first order differential equation. That numerical technique is called Euler's Method. Our initial value problem,
$$\frac{dy}{dx} = f(x,y), \quad y(x_0) = y_0 \qquad (1)$$The Method
An overview of the method is given in the illustration below.
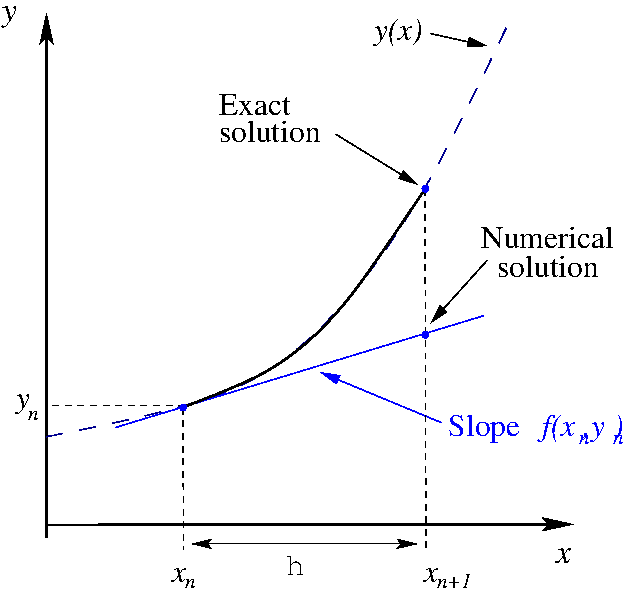
We begin the process described above at the initial condition \( (x_0,y_0) \), then we follow the
straight line with slope \( f(x_0,y_0) \), the tangent line, for some distance to the point \( (x_1,y_1)
\). Follow this process in the Figure 2 below.
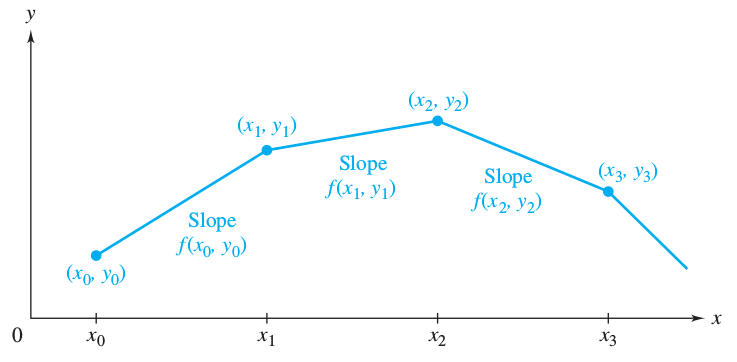
Continuing this same process, we reset the slope to the value \( f(x_1,y_1) \) and follow this line to
\( (x_2,y_2) \). By repeating this process, we construct a piece-wise linear approximation to the
solution. Geometrically, we think of the method as producing a sequence of tiny line segments
connecting \( (x_{n},y_{n}) \) to \( (x_{n+1},y_{n+1}) \). At each step in the process we make a slight
error, as illustrated in Figure 1 above.
To put Euler's Method into practice, we need a formula for determining \( (x_{n+1},y_{n+1}) \) from \( (x_{n},y_{n}) \). Finding \(x_{n+1}\) is easy, we let \(h\) be a fixed positive number, called the step size, so
$$x_{n+1} = x_{n} + h$$To determine \(y_{n+1} \) from \( (x_{n},y_{n}) \), we use the differential equation. We know that
the slope of the solution to the equation \( \frac{dy}{dx} = f(x,y)\) at the point \( (x_{n},y_{n}) \)
is \( f(x_{n},y_{n}) \), and Euler's Method uses this slope to determine \(y_{n+1} \).
The method determines the point \( (x_{n+1},y_{n+1}) \) by assuming that it lies on the line through
\( (x_{n},y_{n}) \) with slope \( f(x_{n},y_{n}) \), see Figure 3 below.
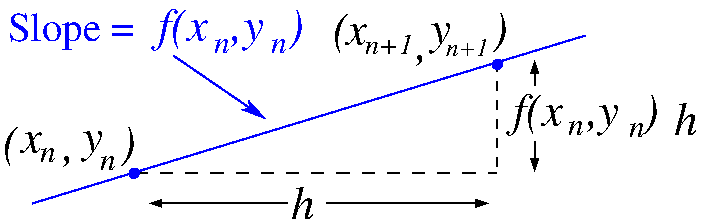
Thus, Euler's Method can be summarized by the recursive formulas
$$x_{n+1} = x_{n} + h \qquad (2) \\ y_{n+1} = y_{n} + h f(x_{n}, y_{n}) \qquad (3) $$An Example
Use Euler's Method to approximate solutions to the initial value problem
$$\frac{dy}{dx} = -1.2y + 7e^{-0.3x}, \quad y(0) = 3 $$ on the interval \( [0,2.5] \).Warm up, do this by hand using \( h = 0.5\)
[let's do the work]
We also wish to compare our numerical results with the exact (analytical) solution:
$$y = \frac{70}{9} e^{-0.3x} - \frac{43}{9} e^{-1.2x} $$| \(n \) | 1 | 2 | 3 | 4 | 5 | 6 |
| \(x_n\) | 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| \(y_n\) (numerical) | 3.0 | 4.700 | 4.892 | 4.550 | 4.052 | 3.542 |
| \(y_n\) (exact) | 3.0 | 4.072 | 4.323 | 4.170 | 3.835 | 3.436 |
| Error | 0.0 | -0.6277 | -0.5696 | 0.3803 | -0.2165 | -0.1054 |
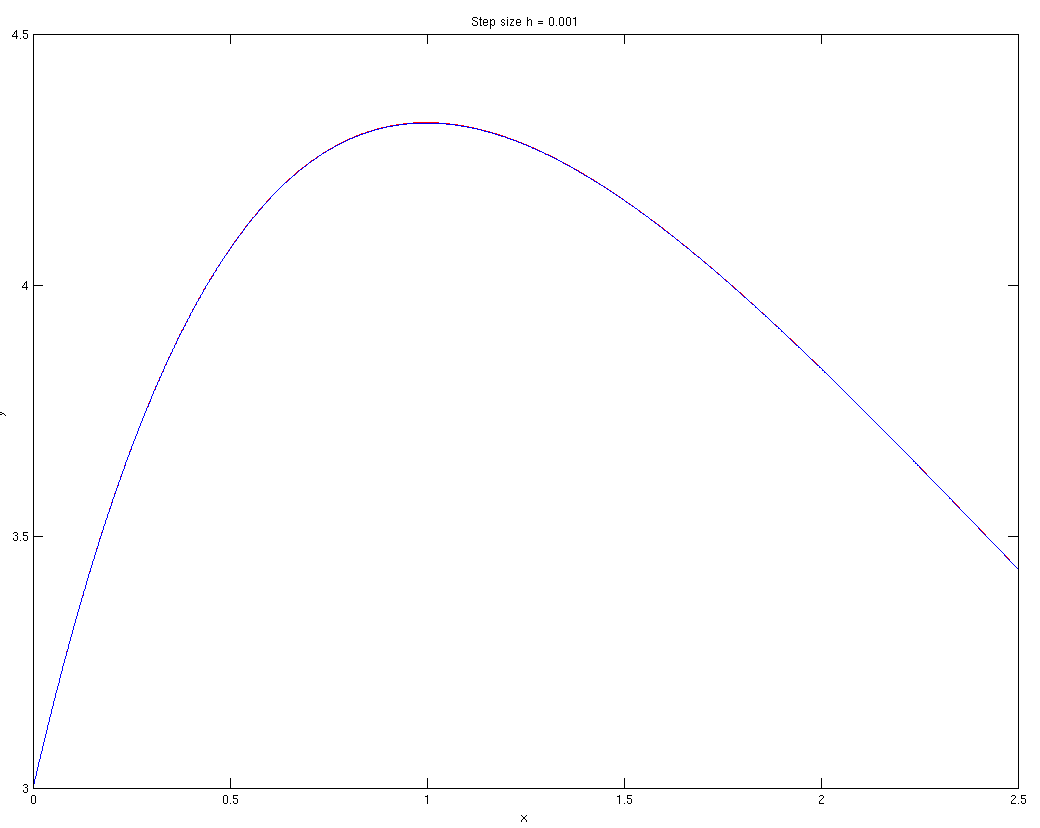
Below is a graph of the actual solution along with the points we calculated above.
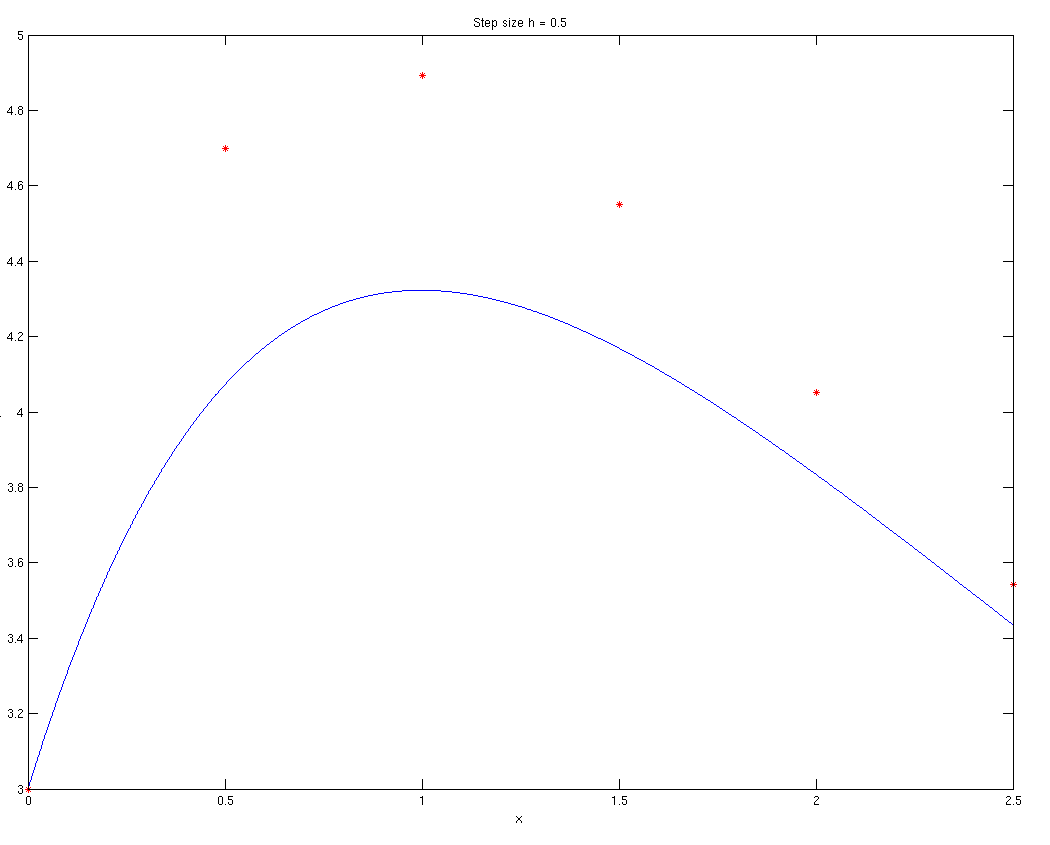
Past this step size, the work is too tedious for hand calculations, we will continue this example using MATLAB (or use a spreadsheet).
If we decrease the step size to \( h = 0.05\), we see much better results.
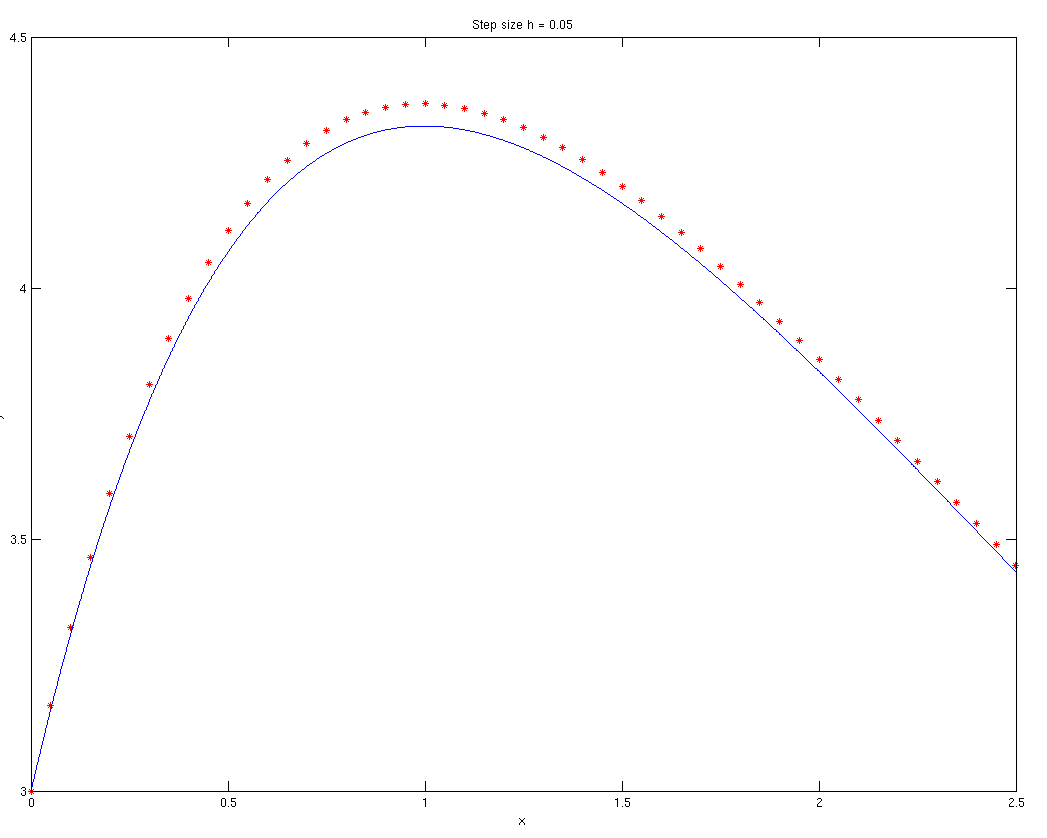
If we further decrease the step size to \( h = 0.001\), we continue to see much better results.