Transformations in Three Dimensions
(And a segue into the fourth)Stretching, Scaling, and Shearing
We can scale or skew three dimensional figures the same way we'd scale or skew two dimensional figures, just using a larger matrix.
Example:
The matrix $$ \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}$$ doubles the first coordinate of each point, stretching all shapes horizontally (by a factor of 2).
The matrix $$ \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}$$ doubles the first coordinate of each point, stretching all shapes horizontally (by a factor of 2).
Stretching, Scaling, and Shearing
We can scale or skew three dimensional figures the same way we'd scale or skew two dimensional figures, just using a larger matrix.
Example:
The matrix $$ \begin{bmatrix} 2 & 0 & 0\\0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ also doubles the first coordinate of each point, and also stretches the space horizontally by a factor of 2.
The matrix $$ \begin{bmatrix} 2 & 0 & 0\\0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ also doubles the first coordinate of each point, and also stretches the space horizontally by a factor of 2.
Stretching, Scaling, and Shearing
We can scale or skew three dimensional figures the same way we'd scale or skew two dimensional figures, just using a larger matrix.
Example:
The matrix $$ \begin{bmatrix} 1 & 0 & 1\\0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ will shear 3D space...
The matrix $$ \begin{bmatrix} 1 & 0 & 1\\0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}$$ will shear 3D space...
Stretching, Scaling, and Shearing
Shearing a cube gives us a parallelepiped:The base stays where it was, but we pushed the top over.
Stretching, Scaling, and Shearing
Shearing a cube gives us a parallelepipedYou might have a parallelepiped with you right now!

Matrix Transformations
All of the transformations we've seen so far can be written as a matrix.If we transform a 2D shape, we use a \(2\times 2\) matrix.
$$ \begin{bmatrix} a&b\\c&d \end{bmatrix}$$
If we transform a 3D shape, we use a \(3\times 3\) matrix.
$$ \begin{bmatrix} a&b&c\\d&e&f\\g&h&i \end{bmatrix}$$
What Can't We Do With Matrices?
We can't translate a shape this way; that is, move it somewhere else.To translate a 2D, we need to add the same value to each \(x\) and \(y\) coordinate.
Example:
$$ \begin{bmatrix} x\\y \end{bmatrix} + \begin{bmatrix} 3\\0 \end{bmatrix} = \begin{bmatrix} x+3\\y \end{bmatrix}$$ will translate the plane 3 units to the right.
$$ \begin{bmatrix} x\\y \end{bmatrix} + \begin{bmatrix} 3\\0 \end{bmatrix} = \begin{bmatrix} x+3\\y \end{bmatrix}$$ will translate the plane 3 units to the right.
What Can't We Do With Matrices?
A 2D translation is an example of an affine transformation, which can't be written as a \(2\times 2\) matrix.
But all hope is not lost for the fans of linear transformations!
We can write a 2D translation as a matrix... we just need an extra dimension.
We can write a 2D translation as a matrix... we just need an extra dimension.
2D Translation Matrix
This matrix: $$ \begin{bmatrix} 1 & 0 & a\\0 & 1 & b\\0 & 0 & 1 \end{bmatrix}$$ will translate the 2D plane \(a\) units to the right and \(b\) units up.The only problem is, we can't multiply this matrix by a vector with only two components, like \(\begin{bmatrix} x\\y \end{bmatrix}\).
2D Translation Matrix
The trick is to use a dummy coordinate. Instead of writing the point \((x,y)\) as a vector with two numbers, we'll write it like this:$$ \begin{bmatrix} x\\y\\1 \end{bmatrix}$$
2D Translation Matrix
Now when we multiply, we'll get another vector with a dummy coordinate, that we'll just ignore:$$ \begin{bmatrix} 1 & 0 & a\\0 & 1 & b\\0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} x+a\\y+b\\1 \end{bmatrix}$$
2D Translation Matrix
Example:
$$ \begin{bmatrix} 1 & 0 & 3\\0 & 1 & 1\\0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} x+3\\y+1\\1 \end{bmatrix}$$ will move every point 3 units to the right and 1 unit up.
$$ \begin{bmatrix} 1 & 0 & 3\\0 & 1 & 1\\0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix} = \begin{bmatrix} x+3\\y+1\\1 \end{bmatrix}$$ will move every point 3 units to the right and 1 unit up.
What About 3D?
We can find a translation matrix for 3D space too.As you might guess, we'll need a \(4 \times 4\) matrix.
$$ \begin{bmatrix} 1 & 0 & 0 & a\\0 & 1 & 0 & b\\0 & 0 & 1 & c \\ 0 & 0 & 0 &1 \end{bmatrix}$$
The Math Checks Out
Algebraically, we have no problem with this.The math works the same way it always did:
$$ \begin{bmatrix} 1 & 0 & 0 & 2\\0 & 1 & 0 & -3\\0 & 0 & 1 & 5 \\ 0 & 0 & 0 &1 \end{bmatrix}\begin{bmatrix} x\\y\\z\\1 \end{bmatrix}=\begin{bmatrix} x+2\\y-3\\z+5\\1 \end{bmatrix}$$
So What's the Big Deal?
The math works, but we've now created something that we don't really understand: a matrix from 4 dimension space.Which begs the question: just what is 4D space?
Before There Were Matrices
Matrices sort of existed in the 1800s, but they were called arrays, and were not thought of as functions yet.They were mainly used to solve systems of linear equations (their big use in linear algebra classes today).
The bracket notation we use now didn't come along until 1913, and took awhile to be adopted.
Before There Were Matrices
Rotations in two dimensions were understood, but used complex numbers.In fact, this is how complex numbers started being taken seriously by mathematicians!
To see how this worked, think of a point \((x,y)\) as a complex number, \(x+iy\). If we multiply this number by \(i\), we get $$i(x+iy) = xi + i^2y = xi-y = -y + ix$$ which we can think of as the point \((-y,x)\).
Before There Were Matrices
Example:
The point \(P = (2,3)\) becomes the complex number \(2+3i\). Multiplying by \(i\) we get $$ i(2+3i) = 2i + 3i^2 = 2i - 3 = -3 + 2i$$ which is the point \(P' = (-3,2)\).
The point \(P = (2,3)\) becomes the complex number \(2+3i\). Multiplying by \(i\) we get $$ i(2+3i) = 2i + 3i^2 = 2i - 3 = -3 + 2i$$ which is the point \(P' = (-3,2)\).
Before There Were Matrices
Example:
Similarly, the point \(Q = (3,2)\) becomes the complex number \(3+2i\). Multiplying by \(i\) we get $$ i(3+2i) = 3i + 2i^2 = 3i - 2 = -2 + 3i$$ which is the point \(Q' = (-2,3)\).
Similarly, the point \(Q = (3,2)\) becomes the complex number \(3+2i\). Multiplying by \(i\) we get $$ i(3+2i) = 3i + 2i^2 = 3i - 2 = -2 + 3i$$ which is the point \(Q' = (-2,3)\).
Before There Were Matrices
So multiplying by \(i\) rotates the plane 90 degrees, just like a matrix can do.We're Still in 2D
Remember, a complex number like \(a+bi\) has two parameters, \(a\) and \(b\), so it's a "two dimensional number".This makes sense, because we only need a two dimensional matrix to rotate.
Rotating in 3D
Rotations in 2D using complex numbers was pretty well understood in the 1800s.
Sir William Rowan Hamilton (1805 – 1865) was an Irish mathematician that tried to find a similar way of rotating 3D shapes.
Sir William Rowan Hamilton (1805 – 1865) was an Irish mathematician that tried to find a similar way of rotating 3D shapes.

Rotating in 3D
He tried adding another imaginary component, something like
$$ a + bi + xj $$
but the math never worked out consistently.
He was about to give up, when he went for a walk...
He was about to give up, when he went for a walk...

Rotating in 3D
While crossing a bridge in 1843, he had a revelation: he needed 3 imaginary numbers to make it work.
He got so excited he carved his idea right into the bridge. His "note to self" is worn away, but this plaque is still there to commemorate the moment.
He got so excited he carved his idea right into the bridge. His "note to self" is worn away, but this plaque is still there to commemorate the moment.

Hamilton's Discovery
Hamilton realized that in order to rotate 3D shapes, he needed to use a number that looked like this:$$ a + bi + cj + dk$$
We won't worry much about the meaning of this number, but \(i\), \(j\) and \(k\) are all "imaginary".
The numbers of this form are called quaternions, and turn out to be really important in physics.
Hamilton's Discovery
What's important to us is that$$ a + bi + cj + dk$$
has four parameters: \(a\), \(b\), \(c\), and \(d\).
It's a four dimensional number!
Fourth Dimension?
Now we have four dimensional numbers and four dimension matrices, and they're being used for real purposes: rotating and moving things in the space we live in.There must be a meaning behind them, but what?
Fourth Dimension = Space?
It could be that the fourth dimension is another dimension of space. The problem is that we don't know where to put it.The three axes we know about are perpendicular, there's no room for another one!
Let's Start Smaller
Every direction we can measure is a dimension. In our universe, we can move up-down, left-right, and back-forth.Those are our three dimensions.
Let's Start Smaller
In the plane, we only have two dimensions: up-down and left-right.Let's Start Smaller
In one-dimensional space, we're stuck on a line, and can only go left-right.Let's Start Smaller
In zero-dimensional space, we can't go anywhere. It's only a point.(Note: not to scale, we actually can't see a point).
A cube is a cube, unless it isn't
We have zero dimensional shapes, but they're all the same: just a point.That's a nice cube!
A cube is a cube, unless it isn't
One dimensional shapes are all pretty much the same too: line segments of different lengths.To make a 1D cube, make two copies of the 0D cube, and connect with a line:
A cube is a cube, unless it isn't
To make a 2D cube, make two copies of the 1D cube, and connect with lines:We usually call this a square!
A cube is a cube, unless it isn't
To make a 3D cube, make two copies of the 2D cube, and connect with lines:At least we see the cube now.
A cube is a cube, unless it isn't
To make a 4D cube, make two copies of the 3D cube, and connect with lines:In mathematics, this is referred to as a tangled mess.
4D Cubes
There is a 4 dimensional cube, but we can't really picture it.To begin to understand pictures of it, we need to remember that we're only seeing a projection.
Even a 3D model of a 4D cube isn't accurate, and a 2D model is worse.
4D Cubes
Another thing to remember is that lines that appear to cross in a projection may not actually cross in reality. Also, the angle between lines isn't accurate.The lines that seem to "cross" here don't really go near each other!
Projections Again
We had some strategies for dealing with the disadvantages of projections. One was to look at multiple views of the object.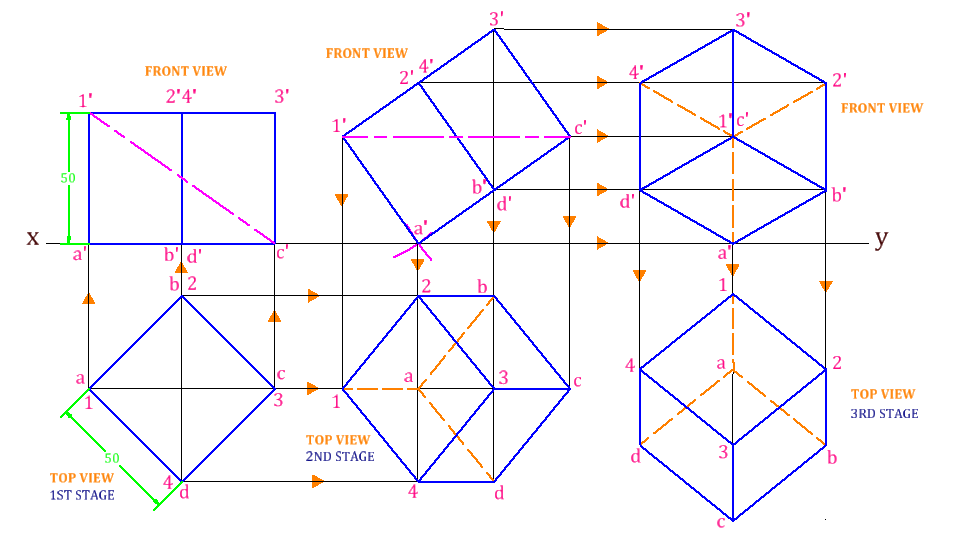
4D Cube Projections
So here's some projections of the 4D Cube: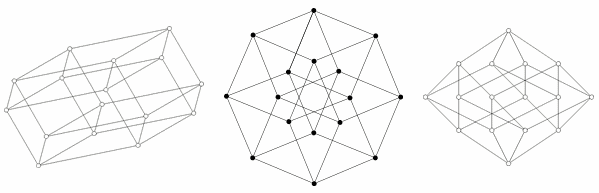
That might not help much, but it's a start.
Projections Again
Another strategy was to rotate the object in the projection:
4D Cube Projections
Let's try rotating the 4D cube, which is called a tesseract:
4D Cube Projections
Here's a stereoscopic rotating projection, about the best we'll ever have!
Hold Still!
Now for a still tesseract again.
There's something important about this that's easy to miss. The edges of the cube that meet at any corner are all perpendicular.
Hold Still!
Now for a still tesseract again.
Not only that, but each of the "inner cells" are all the same size - and they're all 3D cubes. 7 of them, to be exact.
Hold Still!
Now for a still tesseract again.
The big cube surrounding them all? It's the same size as the little cube inside!
But is it real?
What good is a tesseract if we can never build or see one?Does that mean it doesn't exist?
But is it real? YES!
We can't see a point either, but we know they exist. We can't see a line, but we know they exist.We can't even see an actual circle, but they exist!
But is it real? YES!
A tesseract is real. It's a 4 dimensional cube, with 16 corners, 32 edges, 24 faces, and 8 cells (sometimes it's called an 8 cell).It even has an entire Wikipedia page.
By the way, a tesseract can also be called a hypercube, but that name refers to a cube in any number of dimensions. There's cubes in 5, 6, 7, and even more dimensions.
What's Next?
The idea of the fourth dimension generated a lot of interest around 1900. We'll look at the different theories on what it is and how to think about it, and how these theories were embraced by artists.
Until then, here's Salvador Dali holding his beloved tesseract.
Until then, here's Salvador Dali holding his beloved tesseract.
